Масштабом
называется отношение длины линии на плане (карте) к длине горизонтального проложения соответствующей линии на местности.
В свою очередь,
горизонтальным проложением линии
называется проекция соответствующей наклонной линии на местности на горизонтальную плоскость.
С помощью масштаба решаются две задачи: 1 — определение длины линии на топографическом плане (карте); 2 — построение заданной линии на топографическом плане (карте).
Применяется три типа масштаба:
численный, линейный и поперечный.
Продолжить
Численным масштабом
называется масштаб, который выражается дробью, числитель которой равен единице, а знаменатель показывает, во сколько раз горизонтальное проложение линии местности уменьшено при изображении горизонтального проложения линии на плане или карте.
Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.
Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности.
Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е.
50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.
При работе с планом в ряде случаев пользуются линейным масштабом.
Линейный масштаб
— графическое построение, (рис. 1) которое является изображением определенного численного масштаба.

Рис.1
Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.
Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.
Пример: для линейного масштаба (использующегося при работе на топографическом плане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.
Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.
Более точное графическое определение и построение длин линий можно сделать с помощью другого графического построения — поперечного масштаба (рис. 2).
Поперечный масштаб
– графическое построение для максимально точного измерения и откладывания расстояний на топографическом плане (карте). Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба.
Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1 мм. На местности эта величина будет уже равна 0.
1 мм х М, где М – знаменатель масштаба
Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм.
Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).
Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.
Пример: отрезок ав (рис. 2), взятый с плана масштаба 1:2000, соответствует на местности 137,6 м (3 основания поперечного масштаба (3х40=120 м), 4 наименьших деления основания (4х4=16 м) и 4 наименьших деления масштаба (0.4х4=1.6 м), т.е. 120+16+1.6=137.6 м) .
Остановимся на одной из важнейших характеристик понятия «масштаб».
Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба.
Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм.
На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.
Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.
Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.
Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба.
Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики.
Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.
Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.
Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.
- Линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых выражается в масштабе карты, но ширина значительно превышает их фактическую ширину.
- Площадные условные знаки — картографические условные знаки, применяемые для заполнения площадей объектов, выражающихся в масштабе карты.
- Внемасштабные линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых не выражается в масштабе карты.
- Внемасштабные площадные условные знаки — картографические условные знаки, применяемые для изображения объектов, площади которых не выражаются в масштабе карты (плана).
- Пояснительные подписи — подписи, поясняющие вид или род изображенных на карте объектов, а также их количественные и качественные характеристики.
- Штриховые элементы карты (плана) — элементы карты (плана), выполненные линиями, штрихами или точками.
- Фоновые элементы карты (плана) — элементы карты (плана), выполненные каким-либо цветовым фоном.
Скачать условные знаки для топографических планов:
По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.
Определение прямоугольных координат точек
На топографических планах наносится координатная сетка, образующая квадраты со сторонами 10 см. Вертикальные линии сетки параллельны оси абсцисс, а горизонтальные — оси ординат. Координаты вершин квадратов координатной сетки подписываются. Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Пример: запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.
Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
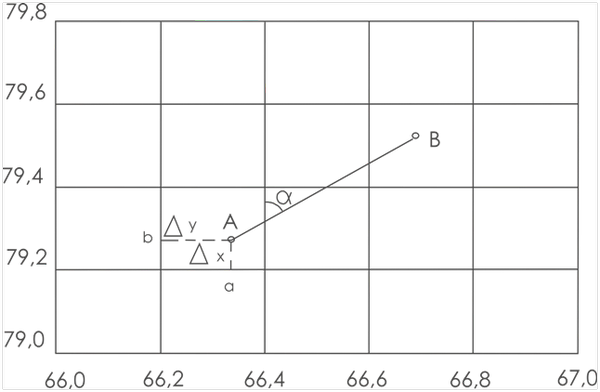
Пример: пользуясь координатной сеткой, циркулем и поперечным масштабом, по топографическому плану можно определить прямоугольные координаты точки А (рис. 4), находящейся в квадрате 79,2 – 66,2. Необходимо помнить, что абсциссы возрастают к северу, а ординаты — к востоку.
Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м.
Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба.
Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.
Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.
Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.
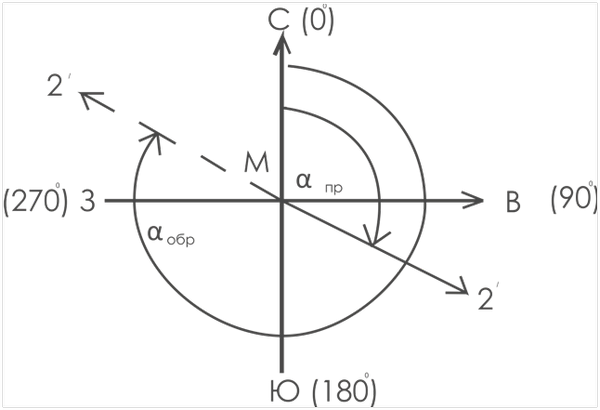
Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана, по ходу часовой стрелки, до направления данной линии.
Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α1, α2, α3, и α4 четырех линий М-1, М-2, М-3, М-4.
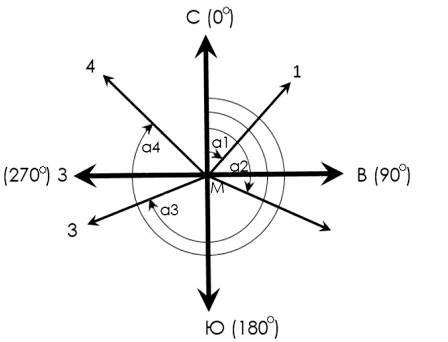
Рис.5
Дирекционный угол заданного направления α пр называется прямым, а противоположного – обратным α обр (рис. 6).

Рис.6
Связь между прямым и обратным дирекционными углами выглядит так:
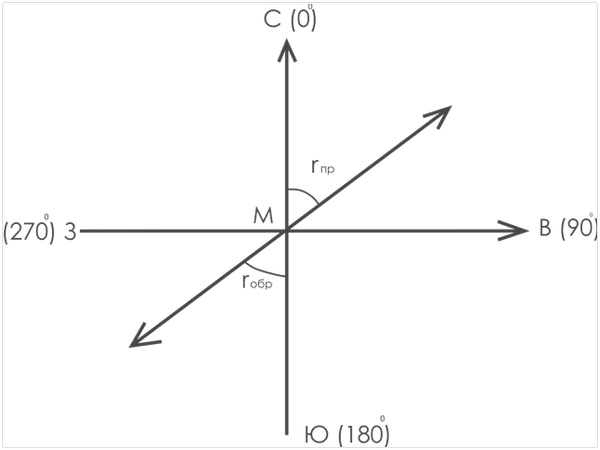
Румбом (r) называется острый горизонтальный угол между северным или южным направлением оси ОХ координатной сетки и направлением данной линии.
Румбы могут иметь значения от 0 до 90 градусов и сопровождаются названием четверти, в которой находится линия. На рис. 7 показаны румбы четырех линий М-1, М-2, М-3, М-4.
Румбы этих линий записывают: СВ: r1; ЮВ: r2; ЮЗ: r3; и СЗ: r4, где, например, СВ — наименование румба, а r1 — значение румба. Например, так выглядит записанный румб: ЮВ: 30º15'

Рис.7
Румб заданного направления r пр. называется прямым, а противоположного – обратным r обр. Прямой и обратный румбы равны по величине и отличаются только наименованием (рис. 8).
Например, если прямой румб равен r пр = СВ: 350º, то обратный румб равен r обр= ЮЗ: 350º.
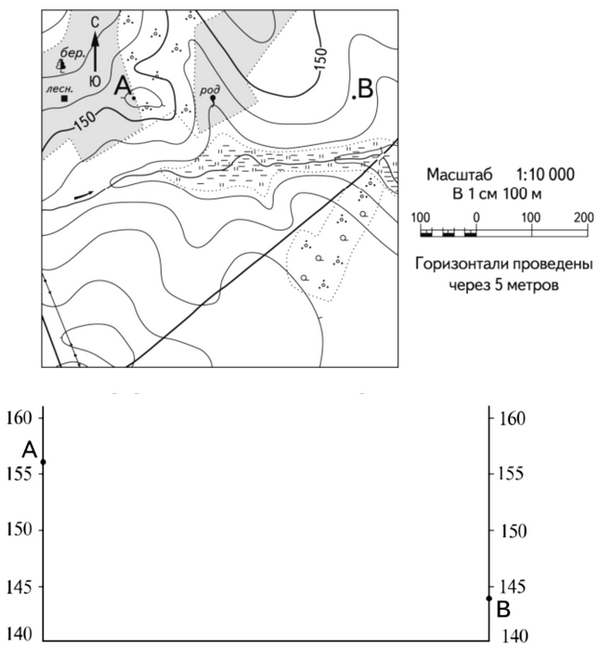
Рис.8
Таблица перехода от дирекционных углов α к румбам r приведена ниже.
Формулы перехода от дирекционных углов к румбам
Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.
Например, Н(А) = A(a) – высота точки А над уровенной по-верхностью PQ, Н(В) = B(b) — высота точки B над уровенной по-верхностью PQ (рис. 9).
Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.
На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.
Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.
Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).
Рис.9
По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис.
10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10).
Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле
Рис.10
Крутизна ската — это угол, образуемый направлением ската с горизонтальной плоскостью в данной точке А. Уклон u линии местности – это тангенс угла наклона ν линии местности (тангенс крутизны ската) к горизонтальной плоскости (рис. 11).
- Рис.11
- Чем больше угол наклона, тем скат круче.
- Для нашего примера уклон линии местности между горизонталями равен
Скачать примеры (docx file) Скачать пустой шаблон (docx file) Пройти тест
Измерение расстояний и определение площадей по топографической карте, численный, линейный и поперечный масштаб
Чтобы произвести измерение расстояний потопографической карте, пользуются численным, линейным или поперечным масштабом. Расстояния между точками на топографической карте обычно измеряются циркулем-измерителем или курвиметром.
Численный масштаб топографической карты
Это масштаб карты выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее степень уменьшения на карте линий местности.
Чем меньше знаменатель масштаба, тем крупнее масштаб карты.
Подпись численного масштаба на картах обычно сопровождается указанием величины масштаба – расстояния на местности (в метрах или километрах), соответствующего одному сантиметру карты.
Например 1:50 000 – в 1 сантиметре 500 метров. Величина масштаба в метрах соответствует знаменателю численного масштаба без двух последних нулей. При определении расстояния с помощью численного масштаба линия на карте измеряетсялинейкой, полученный результат в сантиметрах умножается на величину масштаба.
Линейный масштаб топографической карты
Линейный масштаб – графическое выражение численного масштаба. Он представляет собой прямую линию, разделенную на определенные части, которые сопровождаются подписями, означающими расстояния на местности.
Поперечный масштаб топографической карты
Поперечный масштаб – график (обычно на металлической пластинке) для измерения и откладываниярасстояний на карте с предельной графической точностью (0,1 мм).
Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм.
Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй – 0,4 мм, по третьей – 0,6 мм и т. д.

С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба. Отсчет расстояния по поперечномумасштабу состоит из суммы отсчета на основании графика и отсчета отрезка между вертикальной и наклонной линиями. На рисунке выше, расстояние между точками А и В (при масштабе карты 1:100 000) равно 5500 метров (4 км + 1400 м + 100 м).
Измерение расстояний на карте циркулем–измерителем
При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратамкоординатной сетки, а остаток – обычным порядком по масштабу.
Измерение расстояний на карте способом наращивания раствора циркуля

Измерение расстояний на карте шагом циркуля

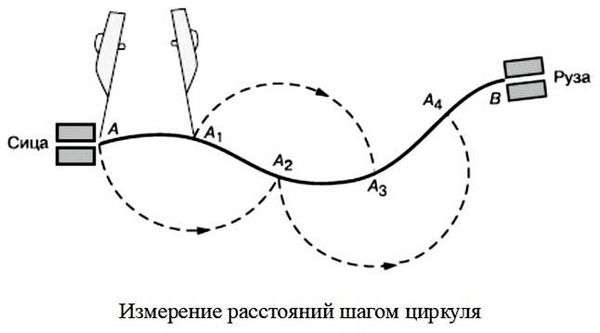
Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками. Измерение расстояний и длин кривых линий производится последовательным отложением шага циркуля. Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.
Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой. Поэтому в результаты измерений покарте приходится вводить поправку – коэффициенты увеличения расстояний.
Измерение расстояний на карте курвиметром
Вращением колесика стрелкукурвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии с равномерным нажимом слева направо или снизу вверх. Полученный отсчет в сантиметрах умножают на величину масштаба данной карты.
Определение расстояний по прямоугольным координатам точек
Определение расстояний попрямоугольным координатам точек в пределах одной зоны карты можно произвести по формуле
где D – длина линии, x1, y1 – координаты начальной точки прямой, x2, y2 – координаты конечной точки прямой.
Определение площадей по квадратам километровой сетки карты
Площадь участка определяется подсчетом целых квадратов и их долей, оцениваемых на глаз. Каждому квадрату километровой сетки соответствует: на картах масштаба 1:25 000 и 1:50 000 – 1 км2, на картах масштаба 1:100 000 – 4 км2, на картах масштаба 1:200 000 – 16 км2.
По материалам книги Способы автономного выживания человека в природе. Под редакцией Л. А. Михайлова.
Масштаб карты
Задачи из экзаменов по географииЗадача 1.

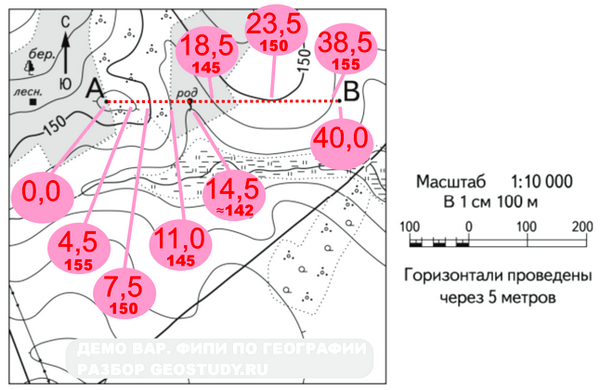
Определите по карте расстояние на местности по прямой от родника до дома лесника. Полученный результат округлите до десятков метров. Ответ запишите в виде числа.
(демоверсия ФИПИ ЕГЭ по географии; в демоверсии ОГЭ задание аналогично)Решение:Найдем указанные объекты и измерим расстояние между ними (красный пунктир). На распечатке в оригинальном размере при измерении линейкой это расстояние 27 мм (2 см 7 мм).Через пропорцию найдем соответствующее расстояние на местности:1 см = 100 м2,7 см = х мх = (2,7 см * 100 м) / 1 см = 270 м.
(округлять не пришлось, но если бы получили 273м или 267 м, то округляем, согласно условию задачи до десятков метров — 270 м).
Ответ согласно условию задачи записываем без размерных единиц.
Ответ: 270
Задача 2.
С корабля, находящегося в точке с координатами 13° с.ш. 73° з.д., поступило радиосообщение о неисправности двигателя. Какое расстояние (в км) до неисправного судна пройдёт ремонтный корабль из порта Риоача (11° с.ш. 73° з.д.), если известно, что корабль будет идти строго по меридиану, а неисправное судно останется в той же точке, откуда было передано сообщение? Запишите решение задачи. Ответ округлите до целого числа.(демоверсия ФИПИ ЕГЭ по географии)Решение:Согласно условию задачи корабль будет двигаться строго по меридиану 73° з.д., и пройдет путь с 11° с.ш. до 13° с.ш., т.е. расстояние, соответствующее 2° длины меридиана.
Длина 1° любого меридиана примерно 111 км
(критерии оценки ФИПИ позволяют использовать длину дуги 1° меридиана от 111,0 до 111,7 км, рекомендуется брать значение 111 км)Необходимо записать в решение подсчёт:(13 — 11) * 111 км = 222 км
(округлять не пришлось, но если бы получили 222,2 км (взяв за длину 1° 111,1 км), то согласно условию задачи нужно округлить до целого — 222 км)
Ответ: 222 км
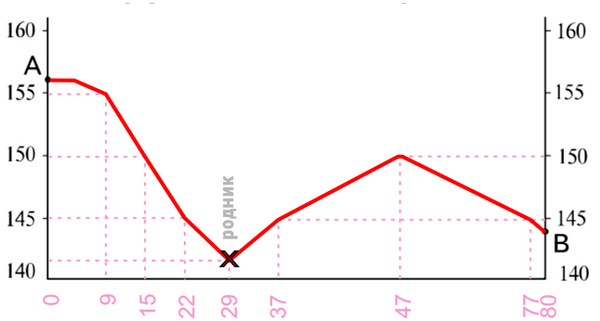
Постройте профиль рельефа местности по линии А – В. Для этого перенесите основу для построения профиля на бланк ответов, используя горизонтальный масштаб в 1 см 50 м и вертикальный масштаб в 1 см 5 м.Укажите на профиле знаком «Х» положение родника.(демоверсия ФИПИ ЕГЭ по географии, в демоверсии ОГЭ задача проще — вместо построения предложено выбрать правильный профиль из вариантов ответов)Решение:1) Сделаем построения на рисунке из условия

1) Соединим т. А и т. B и измерим длину отрезка.В распечатке длина составляет 40 мм.Промерим расстояния относительно точки А в мм, где отрезок пересекает горизонтали, в этих точках нам известны точные высоты — значения этих горизонталей.
2) Построим в бланке ответов заготовку для профиля с высотными положениями т. А и т. B и вертикальной шкалой по образцу, приведенному в задании, соблюдая масштаб вертикальной оси в 1 см 5 м. Т.к. горизонтальный масштаб профиля по условию — в 1 см 50 м (в 2 раза крупнее, чем карты), то длина построенного профиля 40 мм * 2 = 80 мм, все значения, где линия AB пересекает горизонтали и родник также удваиваем и наносим на горизонтальную шкалу и проводим асимптоты до соответствующих высот, по которым строится профиль.
Крестиком отмечаем родник.
Задачи из экзаменов и школьной программы по математикеЗадача 1.
Масштаб карты 1:200 000. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 2,5 см?Решение:Масштаб 1:200 000, т.е. в 1 см 200 000 смили в 1 см 2 кмСоставим пропорцию:1 см = 2 км2,5 см = x кмx = (2,5 см * 2 км) / 1 смx = 5 (км)
Ответ: 5 км.
Задача 2.Отрезку на карте, длина которого 2,4 см, соответствует расстояние на местности в 96 км. Каково расстояние между городами, если на этой карте между ними 15 см?Решение:Составим пропорцию:2,4 см = 96 км15 см = x кмx = (15 см * 96 км) / 2,4 смx = 600 (км)
Ответ: 600 км.
Задача 3.
Расстояние на местности в 75 км изображено на карте отрезком 1,5 см. Определите масштаб карты (именованный и численный).Решение:Составим пропорцию:1,5 см = 75 км1 см = x кмx = (1 см * 75 км) / 1,5 смx = 50 (км)следовательно в 1 см 50 кмили в 1 см 5 000 000 см,т.е. 1:5000000
Ответ: в 1 см 50 км или 1:5000000.
Задача 4.Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1:50000?Решение:4,5 км = 4500 м = 450 000 смСоставим пропорцию:1 см = 50000 смx см = 450000 смx = (450000 см * 1 см) / 50000 смx = 9 (см)
Ответ: 9 см.
Задача 5.Длина железной дороги Москва — Петербург приближенно равна 650 км. Сколько сантиметров займет изображающий ее отрезок в масштабе 1:10 000 000?Решение:Масштаб 1:10000000т.е. 1 см 10000000 см,или в 1 см 100 кмСоставим пропорцию:1 см = 100 кмx см = 650 кмx = (650 км * 1 см) / 100 кмx = 6,5 (см)
Ответ: 6,5 см.
Задача 6.Длина реки на карте в масштабе 1:50000, равна 7,2 см. Чему будет равна длина этой реки на другой карте в масштабе 1:200000?Решение:1) Найдем длину реки на местности по карте масштаба 1:50000:1 см = 50000 см7,2 см = x смиз пропорции x = 360000 (см) — длина реки на местности2) Найдем длину реки на карте 1:200000:1 см = 200000 смx см = 360000 смиз пропорции x = 1,8 (см) — длина реки на второй картеРешение коротким способом:Карта 1:200000 (в 1 см 2 км) мельче карты 1:50000 (в 1 см 500м) в 4 раза (200000/50000 = 4). Следовательно длина реки на второй карте в 4 раза короче: 7,2 см / 4 = 1,8 см.
Ответ: 1,8 см.
Как по масштабу определить расстояние на карте, способы
В топографии принято указывать масштаб тремя способами.
Численный
Численный масштаб относится к самому распространенному виду, применяемому на топографических картах и различных планах. Пишется он в виде: 1:10000, где в числителе единица, а в знаменателе число, указывающее во сколько раз уменьшили реальный объект для указания его на карте. При масштабе 1: 10000 уменьшение будет в 10 тысяч раз.
Обозначение масштаба на карте
Стандартные масштабы:
| Для карт | 1:1000000, 1:500000, 1:300000, 1:200000, 1:100000, 1:50000, 1: 25000, 1:10000 |
| Для планов | 1:5000, 1:2000, 1:1000, 1:500 |
Запомнить нужно, что чем больше цифра после дроби, тем более мелко изображен объект.
Словесный
Словесный масштаб введен для удобства пользователей. Дело в том, что на топографических материалах измерения проводятся в см, но это неудобно людям, которые, говоря о расстояниях, обычно подразумевают метры или километры. Поэтому рядом с числовым может быть написан словесный масштаб. Например, так:
- 1 : 1 000 в 1 см – 10 м,
- 1 : 20 000 в 1 см – 200 м,
- 1 : 5 000 000 в 1 см – 50 км,
- 1 : 75 000 000 в 1 см – 750 км.
Линейный
Дополнительно к числовому, может быть указан линейный масштаб. Он позволяет определить расстояние на карте или наоборот нанести линию на карту без числовых измерений.
Пример линейного масштаба
Линейный масштаб — это линия, которая делится по всей длине на одинаковые отрезки (обычно они равны 2 см). Справа от о у каждой части отрезков указывается расстояние (оно вычисляется согласно существующему масштабу). Слева от нуля также отложен отрезок с более мелкими делениями (обычно их 10).
Чтобы узнать расстояние на карте прикладываем к точке А и точке Б циркуль. Затем полученный раствор переносим на линейный масштаб, чтобы определить расстояние в метрах или километрах.
Справа от нуля устанавливаем конец циркуля на полное значение отрезка, а вторым концом слева от нуля смотрим полученное значение из мелких делений.
Объединив эти два значения, получаем реальное расстояние на местности.
LКарты и компас это азы ориентирования на местности. Как пользоваться компасом, вы узнаете из статьи: Ориентирование по компасу в походе – необходимая азбука для туриста-пешеходника
Измерение расстояний, площадей и углов по карте
Масштабы карт
Масштаб карты показывает, во сколько раз длина линии на карте меньше соответствующей ей длины на местности. Он выражается в виде отношения двух чисел. Например, масштаб 1:50 000 означает, что все линии местности изображены на карте с уменьшением в 50000 раз, т. е. 1 см на карте соответствует 50000 см (или 500 м) на местности.
Масштаб указывается под нижней стороной рамки карты в цифровом выражении (численный масштаб) и в виде прямой линии (линейный масштаб), на отрезках которой подписаны соответствующие им расстояния на местности (рис. 1).
Здесь же указывается и величина масштаба — расстояние в метрах (или километрах) на местности, соответствующее одному сантиметру на карте.
Полезно запомнить правило: если в правой части отношения зачеркнуть два последних нуля, то оставшееся число покажет, сколько метров на местности соответствует 1 см на карте, т. е. величину масштаба.
При сравнении нескольких масштабов более крупным будет тот, у которого число в правой части отношения меньше. Допустим, что на один и тот же участок местности имеются карты масштабов 1:25000, 1:50000 и 1:100000. Из них масштаб 1:25000 будет самым крупным, а масштаб 1:100 000-самым мелким.
Чем крупнее масштаб карты, тем подробнее на ней изображена местность. С уменьшением масштаба карты уменьшается и количество наносимых на нее деталей местности.
- Подробность изображения местности на топографических картах зависит от ее характера: чем меньше деталей содержит местность, тем полнее они отображаются на картах более мелких масштабов.
- В нашей стране и многих других странах в качестве основных масштабов топографических карт приняты: 1:10000, 1:25000, 1: 50000, 1: 100000, 1: 200000, 1: 500000 и 1:1000000.
- Используемые в войсках карты подразделяются на крупномасштабные, среднемасштабные и мелкомасштабные.
Измерение по карте прямых и извилистых линий
Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.
Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 2); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 3).
Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя. В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 2).
Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
Таким же способом измеряют расстояния по извилистым линиям (рис. 4). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.
Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 5), который особенно удобен для измерения извилистых и длинных линий.
В приборе имеется колесико, которое соединено системой передач со стрелкой. При измерении расстояния курвиметром нужно установить его стрелку на деление 99.
Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали.
Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)
Точность измерения расстояний по карте: Поправки на расстояние за наклон и извилистость линий
Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
Наиболее точно определить расстояние по карте можно по прямой линии. При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7-1 мм в масштабе карты, что составляет для карты масштаба 1:25000 — 17,5-25 м, масштаба 1:50000 – 35-50 м, масштаба 1:100000 – 70-100 м.
В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.
Например, При крутизне ската 20° (рис. 6) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.
Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6% (на 100 м прибавлять 6 м), при угле наклона 30° — на 15%, а при угле 40° — на 23%.
При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний. Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах.
Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.
Простейшие способы измерения площадей по карте
Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000 — 1:50000 на местности соответствует 1 км2 , квадрату сетки карт масштаба 1:100000 — 4 км2, квадрату сетки карт масштаба 1:200000 — 16 км2.
Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений). Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта.
Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.
По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников {в гектарах ) указаны на линейке для каждого масштаба гарты.
Азимуты и дирекционный угол. Магнитное склонение, сближение меридианов и поправка направления.
Истинный азимут (Аи) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением истинного меридиана данной точки и направлением на объект (см. рис. 7).
Магнитный азимут (Ам) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0е до 360° между северным направлением магнитного меридиана данной точки и направлением на объект.
Дирекционный угол (α; ДУ) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением вертикальной линии координатной сетки данной точки и направлением на объект. Магнитное склонение (δ; Ск) — угол между северным направлением истинного и магнитного меридианов в данной точке.
Если магнитная стрелка отклоняется от истинного меридиана к востоку, то склонение восточное (учитывается со знаком +), при отклонении магнитной стрелки к западу — западное (учитывается со знаком -).
Сближение меридианов (γ; Сб) — угол между северным направлением истинного меридиана и вертикальной линией координатной сетки в данной точке. При отклонении линии сетки к востоку – сближение меридиана восточное (учитывается со знаком +), при отклонении линии сетки к западу — западное (учитывается со знаком -).
Поправка направления (ПН) — угол между северным направлением вертикальной линии координатной сетки и направлением магнитного меридиана. Она равна алгебраической разности магнитного склонения и сближения меридианов:
Измерение и построение дирекционных углов на карте. Переход от дирекционного угла к магнитному азимуту и обратно.
На местности при помощи компаса (буссоли) измеряют магнитные азимуты направлений, от которых затем переходят к дирекционным углам. На карте наоборот, измеряют дирекционные углы и от них переходят к магнитным азимутам направлений на местности.
Дирекционные углы на карте измеряются транспортиром или хордоугломером.
Измерение дирекционных углов транспортиром производят в следующей последовательности:
— ориентир, на который измеряют дирекционный угол, соединяют прямой линией с точкой стояния так, чтобы эта прямая была больше радиуса транспортира и пересекала хотя бы одну вертикальную линию координатной сетки; — совмещают центр транспортира с точкой пересечения, как показано на рис. 8 и отсчитывают по транспортиру значение дирекционного угла. В нашем примере дирекционный угол с точкой А на точку В равен 274° (рис. 8, а), а с точки А на точку С – 65° (рис. 8, б).
На практике часто возникает необходимость в определении магнитного АМ по известному дирекционному углу ά , или, наоборот, угла ά no известному магнитному азимуту.
Переход от дирекционного угла к магнитному азимуту и обратно
Переход от дирекционного угла к магнитному азимуту и обратно выполняют тогда, когда на местности необходимо с помощью компаса (буссоли) найти направление, дирекционный угол которого измерен по карте, или наоборот, когда на карту необходимо нанести направление, магнитный азимут которого измерен, на местности с помощью компаса.
Как проходит охота на куропатку – советы и полезное видео
Для решения этой задачи необходимо знать величину отклонения магнитного меридиана данной точки от вертикальной километровой линии. Эту величину называют поправкой направления (ПН).
Поправка направления и составляющие ее углы — сближение меридианов и магнитное склонение указываются на карте под южной стороной рамки в виде схемы, имеющей вид, показанный на рис. 9.
Сближение меридианов (g) — угол между истинным меридианом точки и вертикальной километровой линией зависит от удаления этой точки от осевого меридиана зоны и может иметь значение от 0 до ±3°. На схеме показывают среднее для данного листа карты сближение меридианов.
Магнитное склонение (d) — угол между истинным и магнитным меридианами указан на схеме на год съемки (обновления) карты. В тексте, помещаемом рядом со схемой, приводятся сведения о направлении и величине годового изменения магнитного склонения.
Чтобы избежать ошибок в определении величины и знака поправки направления, рекомендуется следующий прием. Из вершины углов на схеме (рис. 10) провести произвольное направление ОМ и обозначить дужками дирекционный угол ά и магнитный азимут Ам этого направления. Тогда сразу будет видно, каковы величина и знак поправки направления.
Если, например, ά = 97°12′, то Ам = 97°12′ — (2°10’+10°15′) = 84°47′.
Подготовка по карте данных для движения по азимутам
Движение по азимутам – это основной способ ориентирования на местности, бедной ориентирами, особенно ночью и при ограниченной видимости.
Сущность его заключается в выдерживании на местности направлений, заданных магнитными азимутами, и расстояний, определенных по карте между поворотными пунктами намеченного маршрута.
Направления движения выдерживают с помощью компаса, расстояния измеряют шагами или по спидометру.
Исходные данные для движения по азимутам (магнитные азимуты и расстояния) определяют по карте, а время движения – по нормативу и оформляют в виде схемы (рис. 11) или вписывают в таблицу (табл. 1).
Данные в таком виде выдают командирам, которые не имеют топографических карт.
Если командир имеет свою рабочую карту, то исходные данные для движения по азимутам он оформляет непосредственно на рабочей карте.
Маршрут движения по азимутам выбирают с учетом проходимости местности, ее защитных и маскировочных свойств, чтобы он обеспечивал в боевой обстановке быстрый и скрытный выход к указанному пункту.
В маршрут обычно включают дороги, просеки и другие линейные ориентиры, которые облегчают выдерживание направления движения. Поворотные пункты выбирают у ориентиров, легко опознаваемых на местности (например, постройки башенного типа, перекрестки дорог, мосты, путепроводы, геодезические пункты и т. п.).
Опытным путем установлено, что расстояния между ориентирами на поворотных пунктах маршрута не должны превышать 1 км при движении днем в пешем порядке, а при движении на машине – 6–10 км.
Для движения ночью ориентиры намечаются по маршруту чаще. Чтобы обеспечить скрытный выход к указанному пункту, маршрут намечают по лощинам, массивам растительности и другим объектам, обеспечивающим маскировку движения. Необходимо избегать передвижений по гребням возвышенностей и открытым участкам.
Расстояния между выбранными на маршруте движения ориентирами на поворотных пунктах измеряют по прямым линиям с помощью циркуля-измерителя и линейного масштаба или возможно точнее – линейкой с миллиметровыми делениями. Если маршрут намечен по холмистой (горной) местности, то в измеренные по карте расстояния вводят поправку за рельеф.





